Ctrl+K

Plimton 322 の解読 (1)

Plimton 322 の解読 (1)#

粘土板に楔形文字を書く#

Plimpton 322 の外観#

fig-2

fig-3

Plimpton 322 の数表を読み込む#

  • Plimpton 322 - Wikipedia

    • 数表-1: 60進法

      • 異なる推定値を括弧で示し、1番目と4番目のコラムのうち内容が推定される破損部分を斜体で示し、6つの推定誤りを太字で示し、その下の角括弧に一般に提案されている訂正を示す

      • 3列目の53を2倍の値である1 46に置き換えるか、2列目の56を半分の値である28に置き換えるか

    • 数表-2: 10進法

      • 11行目の2列目と3列目には、15行目を除く他の行とは異なり、共通因子が含まれている。\(45\) と\(1 15\)はバビロニア数学では\(3/4\)と\(5/4\)と解釈される可能性があり、これはおなじみの標準的な直角三角形 \((3,4,5)\) を縮小した\((0.75, 1, 1.25)\) と一致するものです

      • 15行目も2列目が28、3列目が53と修正される可能性がある

!pip install -U lxml

Requirement already satisfied: lxml in /opt/conda/lib/python3.11/site-packages (5.2.2)

import pandas as pd

dfs=pd.read_html('https://en.wikipedia.org/wiki/Plimpton_322')
dfs[0]
Plimpton 322 Plimpton 322.1
0 The Plimpton 322 clay tablet, with numbers wri... The Plimpton 322 clay tablet, with numbers wri...
1 Height 9 cm
2 Width 13 cm
3 Created c. 1800 BC
4 Present location New York City, New York, United States 
dfs[1]
takiltum of the diagonal from which 1 is torn out so that the width comes up ÍB.SI8 of the width ÍB.SI8 of the diagonal its line
0 (1) 59 00 15 1 59 2 49 1st
1 (1) 56 56 58 14 56 15 (1) 56 56 58 14 [50 06] 15 56 07 3 12 01 [1 20 25] 2nd
2 (1) 55 07 41 15 33 45 1 16 41 1 50 49 3rd
3 (1) 53 10 29 32 52 16 3 31 49 5 09 01 4th
4 (1) 48 54 01 40 1 05 1 37 5th
5 (1) 47 06 41 40 5 19 8 01 6th
6 (1) 43 11 56 28 26 40 38 11 59 01 7th
7 (1) 41 33 59 03 45 (1) 41 33 [45 14] 03 45 13 19 20 49 8th
8 (1) 38 33 36 36 9 01 [8] 01 12 49 9th
9 (1) 35 10 02 28 27 24 26 40 1 22 41 2 16 01 10th
10 (1) 33 45 45 1 15 11th
11 (1) 29 21 54 02 15 27 59 48 49 12th
12 (1) 27 00 03 45 7 12 01 [2 41] 4 49 13th
13 (1) 25 48 51 35 06 40 29 31 53 49 14th
14 (1) 23 13 46 40 56 56 [28] (alt.) 53 [1 46] 53 (alt.) 15th 
dfs[2]
or Short Side Diagonal Row #
0 (1).9834028 119 169 1
1 (1).9491586 3367 4825 2
2 (1).9188021 4601 6649 3
3 (1).8862479 12709 18541 4
4 (1).8150077 65 97 5
5 (1).7851929 319 481 6
6 (1).7199837 2291 3541 7
7 (1).6927094 799 1249 8
8 (1).6426694 481 769 9
9 (1).5861226 4961 8161 10
10 (1).5625 45* 75* 11
11 (1).4894168 1679 2929 12
12 (1).4500174 161 289 13
13 (1).4302388 1771 3229 14
14 (1).3871605 56* 106* 15

11行目に着目する#

dfs[1].take([10])
takiltum of the diagonal from which 1 is torn out so that the width comes up ÍB.SI8 of the width ÍB.SI8 of the diagonal its line
10 (1) 33 45 45 1 15 11th 
dfs[2].take([10])
or Short Side Diagonal Row #
10 (1).5625 45* 75* 11 
import math
math.sqrt(75**2 - 45**2)

60.0

Note

\((45, 60, 75)\)という三数は、\(60\)進法の基数を含むため、古代バビロニア人には応用し易い組み合わせだったと考えられます。

\(10\)進法では、既約表現である\((3, 4, 5)\)を使います。

数表の公式#

正の整数 \(p\), \(q\) \((p>q)\) に対して、

\[\begin{split} \begin{align} a & = 2 p q \\ b & = p^2 - q^2\\ d & = p^2 + q^2\\ \end{align} \end{split}\]

とおくと、\(a\), \(b\), \(d\) はピタゴラスの三数となり、\(a^2+b^2 = d^2\) を満たす。

解) 恒等式

\[ (x-y)^2 = (x+y)^2 - 4xy \]

に対して \(x=p^2\), \(y=q^2\) とおいて \(p\), \(q\) を消去する。

\[\begin{split} \begin{align} (p^2-q^2)^2 &= (p^2+q^2)^2 - 4p^2q^2 \\ b^2 &= d^2 - a^2 \end{align} \end{split}\]

Note

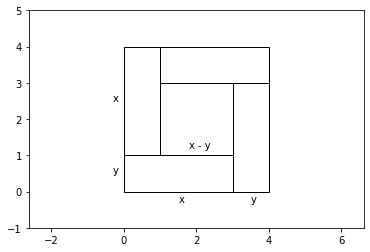
方程式\((2)\)は、次の図の面積の関係を表しています。

from matplotlib.patches import Polygon
import matplotlib.pyplot as plt

p0 = Polygon([(0,0), (3,0), (3,1), (0,1), ], fill=False)
p1 = Polygon([(3,0), (4,0), (4,3), (3,3), ], fill=False)
p2 = Polygon([(4,3), (4,4), (1,4), (1,3), ], fill=False)
p3 = Polygon([(1,1), (1,4), (0,4), (0,1), ], fill=False)

fig, ax = plt.subplots(1,1)

ax.add_patch(p0)
ax.add_patch(p1)
ax.add_patch(p2)
ax.add_patch(p3)
ax.axis('equal')
ax.set(xlim=(0,4),ylim=(-1,5))

plt.text(1.5,-0.3,'x')
plt.text(3.5,-0.3,'y')
plt.text(-0.3,2.5,'x')
plt.text(-0.3,0.5,'y')
plt.text(1.8,1.2, 'x - y')
plt.show()
../../_images/d7a3a19e514611fb38ec3ac16d9989ccdee36790c7d73377438846ae2d8a6857.png

Plimpton 322との対応は次の表の通りである:

#1

#2

#3

$\(\left(\frac{d}{a}\right)^2\)$

$\(b\)$

$\(d\)$

$\(\frac{1}{4}\left(\frac{p}{q}+\frac{q}{p}\right)^2\)$

$\(p^2-q^2\)$

$\(p^2+q^2\)$

命題) Plimpton 322は、互いに素な正の整数 \(p\), \(q\) のうち、

\[ \frac{9}{5} \leq \frac{p}{q} \leq \frac{12}{5} \]

を満たす組み合わせについて、

\[ \frac{d}{a} = \frac{1}{2}\left(\frac{p}{q}+\frac{q}{p}\right) \]

をキーとして降順に並べたものである。

Contents