Ctrl+K

YBC 7289 (2)

YBC 7289 (2)#

Plimpton 322を生成する元となったと考えられる公式#

正の整数 \(p\), \(q\) \((p>q)\) に対して、

\[\begin{split} \begin{align} a & = 2 p q \\ b & = p^2 - q^2\\ d & = p^2 + q^2\\ \end{align} \end{split}\]

とおくと、\(a\), \(b\), \(d\) はピタゴラスの三数となり、\(a^2+b^2 = d^2\) を満たす。

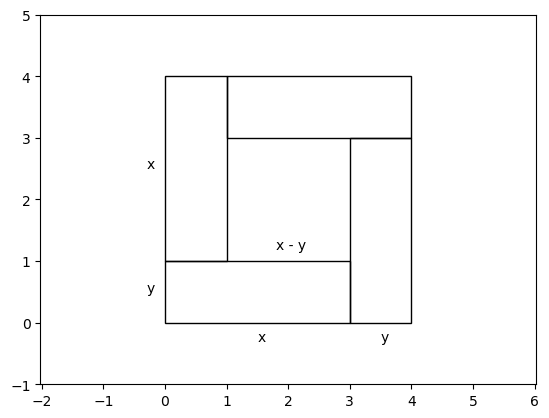
証明) 恒等式

\[ (x-y)^2 = (x+y)^2 - 4xy \]

に対して \(x=p^2\), \(y=q^2\) とおいて \(p\), \(q\) を消去する。

\[\begin{split} \begin{align} (p^2-q^2)^2 &= (p^2+q^2)^2 - 4p^2q^2 \\ b^2 &= d^2 - a^2 \end{align} \end{split}\]

その図形的解釈#

../../_images/20525b84ede87ac7186ee4f50543db4f80366344f0c3c0183bc262f9e9fac77d.png

Euclid’s Element#

Note

  • ユークリッドの原論10巻は、無理数が有理数と同じ数の基本的な性質を持つことが示されています。

  • そして、有理数と無理数の関係を「通約」が可能か否かで論じています。

  • 数の体系を有理数から無理数を含む実数に拡大している現代人には大変理解が難しい議論になっています。

%%ai vioras
ユークリッドの原論における通約可能 (incommensurable) について

ユークリッドの「原論」における「不可測（incommensurable）」とは、2つの長さが共通の単位で測ることができない、つまり比率が無理数になる場合を指します。これは、ユークリッドがギリシャの数学者たちと同様に、数値を長さの比率として理解していたためです。

この概念は、「原論」の第10巻で詳しく説明されています。例えば、一辺が1、他辺が√2の長方形があるとします。この2つの辺の長さは不可測です。なぜなら、ある共通の単位で両者を測ることはできず、その比は無理数であるからです。

この発見は、古代ギリシャの数学者にとっては衝撃的でした。なぜなら、彼らはすべての数が有理数（分数）であると信じていたからです。この発見は、数学の基本的な概念を再考するきっかけとなりました。

なお、ここで使用した「不可測」や「無理数」などの語は、当時のギリシャ語の概念を現代の数学の用語で説明しています。

%%ai vioras
その概念は現代にどう伝わりましたか？

ユークリッドの「不可測」の概念は、現代の数学における「無理数」の概念へと発展しました。古代ギリシャの数学者たちは、数を全て有理数（分数）とみなしていました。しかし、ユークリッドの「不可測」の発見は、すべての数が有理数であるという考え方を覆しました。この発見は、数学者たちによる数の性質についての深い理解へとつながり、現代の実数の概念へと発展しました。

さらに、無理数の存在は、数の連続性という重要な概念を導き出す触媒ともなりました。この概念は、微積分などの現代的な数学の分野で中心的な役割を果たしています。

したがって、ユークリッドの「不可測」の概念は、現代数学の基礎を築く重要な一部となりました。

相加相乗平均#

系) \((x-y)^2 \geq 0\) なので、\((x+y)^2 - 4xy \geq 0\) が成り立つ。これを次のように変形すると、相加相乗平均の公式が得られる。

\[\begin{split} \begin{align} \frac{(x+y)^2}{4} &\geq \ xy \\ \frac{x+y}{2} &\geq \sqrt{xy} \end{align} \end{split}\]

ピタゴラスの定理の証明の一つ#

\[\begin{split} \begin{align} (a-b)^2+4\frac{ab}{2} &= d^2 \\ a^2 + b^2 & = d^2 \end{align} \end{split}\]
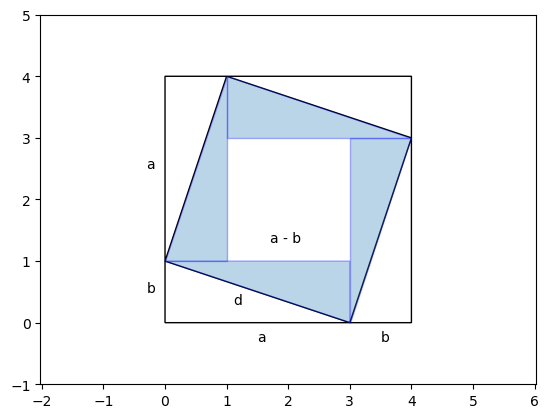
../../_images/7c3385abfe6556252fd7c065ededd2a093b8230e7e2ec8603e3f7cd7b66c61e3.png

\(a=b\)のとき、\(a-b = 0\)なので、YBC7289の図形となる。

Contents