重力と測地線 (2)#
Geodesic#
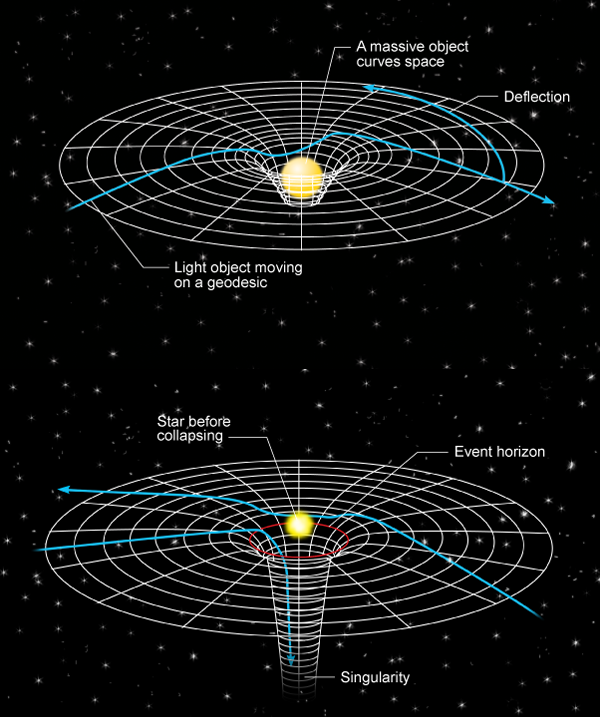
Geodesic equation#
\[
\frac{d^2 x^\lambda}{dt^2}
+ \Gamma^\lambda_{\mu \nu}
\frac{dx^\mu}{dt} \frac{dx^\nu}{dt} = 0
\]
半径 \(r\) の球面を極座標 \((\theta, \phi)\) で表す:
R3_s.base_scalars()
[r, theta, phi]
s = R3_s.transform(R3_r, R3_s.base_scalars())
s
\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(\mathbf{\theta} \right)} \cos{\left(\mathbf{\phi} \right)} \mathbf{r}\\\sin{\left(\mathbf{\theta} \right)} \sin{\left(\mathbf{\phi} \right)} \mathbf{r}\\\cos{\left(\mathbf{\theta} \right)} \mathbf{r}\end{matrix}\right]\end{split}\]
\(\theta\) と \(\phi\) を媒介変数 \(t\) の関数とみなす:
t = Symbol('t')
theta = Function('theta')(t)
phi = Function('phi')(t)
funcs = (theta, phi)
for i in range(2):
display(funcs[i])
\[\displaystyle \theta{\left(t \right)}\]
\[\displaystyle \phi{\left(t \right)}\]
for i in range(2):
display(funcs[i].diff())
\[\displaystyle \frac{d}{d t} \theta{\left(t \right)}\]
\[\displaystyle \frac{d}{d t} \phi{\left(t \right)}\]
for i in range(2):
display(funcs[i].diff().diff())
\[\displaystyle \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}\]
\[\displaystyle \frac{d^{2}}{d t^{2}} \phi{\left(t \right)}\]
測地線の公式に代入する:
\[
\frac{d^2 x^\lambda}{dt^2}
+ \Gamma^\lambda_{\mu \nu}
\frac{dx^\mu}{dt} \frac{dx^\nu}{dt} = 0
\]
chr2.tensor()
\[\begin{split}\displaystyle \left[\begin{matrix}\left[\begin{matrix}0 & 0\\0 & - \sin{\left(\theta \right)} \cos{\left(\theta \right)}\end{matrix}\right] & \left[\begin{matrix}0 & \frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}}\\\frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}} & 0\end{matrix}\right]\end{matrix}\right]\end{split}\]
import itertools
geodesic=[0,0]
for i in range(2):
geodesic[i] = funcs[i].diff().diff()
for j,k in itertools.product((0,1), repeat=2):
geodesic[i] += (chr2[i,j,k] * funcs[j].diff() * funcs[k].diff())
display(geodesic[i])
\[\displaystyle - \sin{\left(\theta \right)} \cos{\left(\theta \right)} \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} + \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}\]
\[\displaystyle \frac{d^{2}}{d t^{2}} \phi{\left(t \right)} + \frac{2 \cos{\left(\theta \right)} \frac{d}{d t} \phi{\left(t \right)} \frac{d}{d t} \theta{\left(t \right)}}{\sin{\left(\theta \right)}}\]
\[\begin{split}
\begin{align}
\theta'' - \sin(\theta) \cos(\theta) (\phi')^2 & = 0 \\
\phi'' + 2 \cot(\theta) \phi' \theta' & = 0
\end{align}
\end{split}\]
測地線は一次元なので、\(\theta\) を \(\phi = \phi(t)\) の関数とみなし、媒介変数 \(t\) で微分する。
theta = Function('theta')(phi)
theta
\[\displaystyle \theta{\left(\phi{\left(t \right)} \right)}\]
display(theta, phi)
\[\displaystyle \theta{\left(\phi{\left(t \right)} \right)}\]
\[\displaystyle \phi{\left(t \right)}\]
phi.diff()
\[\displaystyle \frac{d}{d t} \phi{\left(t \right)}\]
theta.diff(t)
\[\displaystyle \frac{d}{d t} \phi{\left(t \right)} \frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}\]
theta.diff().diff()
\[\displaystyle \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} \frac{d^{2}}{d \phi{\left(t \right)}^{2}} \theta{\left(\phi{\left(t \right)} \right)} + \frac{d^{2}}{d t^{2}} \phi{\left(t \right)} \frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}\]
geodesic=[0,0]
funcs = (theta, phi)
for i in range(2):
geodesic[i] = funcs[i].diff().diff()
for j,k in itertools.product((0,1), repeat=2):
geodesic[i] += (chr2[i,j,k] * funcs[j].diff() * funcs[k].diff())
display(geodesic[i])
\[\displaystyle - \sin{\left(\theta \right)} \cos{\left(\theta \right)} \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} + \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} \frac{d^{2}}{d \phi{\left(t \right)}^{2}} \theta{\left(\phi{\left(t \right)} \right)} + \frac{d^{2}}{d t^{2}} \phi{\left(t \right)} \frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}\]
\[\displaystyle \frac{d^{2}}{d t^{2}} \phi{\left(t \right)} + \frac{2 \cos{\left(\theta \right)} \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} \frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}}{\sin{\left(\theta \right)}}\]
次のように簡略化する:
phi.diff().diff()
\[\displaystyle \frac{d^{2}}{d t^{2}} \phi{\left(t \right)}\]
二つ目の式 geodesic[1] を \(\phi''\) (phi.diff().diff()) について解く:
from sympy.solvers import solve
g1, = solve(geodesic[1], phi.diff().diff())
display(g1)
\[\displaystyle - \frac{2 \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2} \frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}}{\tan{\left(\theta \right)}}\]
一つ目の式 geodesic[0] に代入する:
sympy.simplify(geodesic[0].subs(phi.diff().diff(), g1))
\[\displaystyle \left(- \frac{\sin{\left(2 \theta \right)}}{2} + \frac{d^{2}}{d \phi{\left(t \right)}^{2}} \theta{\left(\phi{\left(t \right)} \right)} - \frac{2 \left(\frac{d}{d \phi{\left(t \right)}} \theta{\left(\phi{\left(t \right)} \right)}\right)^{2}}{\tan{\left(\theta \right)}}\right) \left(\frac{d}{d t} \phi{\left(t \right)}\right)^{2}\]
次の簡略化された測地線の方程式が得られる:
\[
\theta'' - 2 \cot(\theta) (\theta')^2 - \cos(\theta)\sin(\theta) = 0
\]
さらに、\(\omega\) を次のように定義する:
\[
\omega(t) = \cot(\theta(t))
\]
theta = Function('theta')(t)
display(theta.diff(), theta.diff().diff())
\[\displaystyle \frac{d}{d t} \theta{\left(t \right)}\]
\[\displaystyle \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}\]
cot(theta)
\[\displaystyle \cot{\left(\theta{\left(t \right)} \right)}\]
sympy.simplify(cot(theta).diff())
\[\displaystyle - \frac{\frac{d}{d t} \theta{\left(t \right)}}{\sin^{2}{\left(\theta{\left(t \right)} \right)}}\]
sympy.simplify(cot(theta).diff().diff())
\[\displaystyle \frac{2 \cot{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} - \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}}{\sin^{2}{\left(\theta{\left(t \right)} \right)}}\]
omega = Function('omega')(t)
omega
\[\displaystyle \omega{\left(t \right)}\]
display(omega.diff(), omega.diff().diff())
\[\displaystyle \frac{d}{d t} \omega{\left(t \right)}\]
\[\displaystyle \frac{d^{2}}{d t^{2}} \omega{\left(t \right)}\]
\(\omega\) に式を代入してしまうと、\(\omega\) 自身やその微分について、評価を保留して記号として参照できないため、次のように間接的な手法で値を求めていく:
定義式の左辺 \(\cot(\theta(t))\) を微分すると \(\omega'\) : omega.diff() が得られる:
sympy.simplify(cot(theta).diff())
\[\displaystyle - \frac{\frac{d}{d t} \theta{\left(t \right)}}{\sin^{2}{\left(\theta{\left(t \right)} \right)}}\]
上式を solve()を使って \(\theta'\) : theta.diff() について解き、\(\omega'\) で表す:
theta1, = solve(omega.diff() - sympy.simplify(cot(theta).diff()), theta.diff())
display(theta1)
\[\displaystyle - \sin^{2}{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \omega{\left(t \right)}\]
\(\theta' = - \omega' \sin^2(\theta)\) が得られる。
同じように \(\cot(\theta(t))\) を二回微分すると \(\omega''\) : omega.diff().diff() が得られる:
sympy.simplify(cot(theta).diff().diff())
\[\displaystyle \frac{2 \cot{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} - \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}}{\sin^{2}{\left(\theta{\left(t \right)} \right)}}\]
上式を \(\theta''\) : theta.diff().diff() について解き、\(\omega''\), \(\omega'\) で表す:
theta.diff().diff()
\[\displaystyle \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}\]
theta2, = solve(omega.diff().diff() - sympy.simplify(cot(theta).diff()).diff(), theta.diff().diff())
display(theta2)
\[\displaystyle - \sin^{2}{\left(\theta{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \omega{\left(t \right)} + \frac{2 \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2}}{\tan{\left(\theta{\left(t \right)} \right)}}\]
theta2 = sympy.simplify(theta2.subs(theta.diff(), theta1))
theta2
\[\displaystyle \left(2 \sin{\left(\theta{\left(t \right)} \right)} \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \omega{\left(t \right)}\right)^{2} - \frac{d^{2}}{d t^{2}} \omega{\left(t \right)}\right) \sin^{2}{\left(\theta{\left(t \right)} \right)}\]
上で得られた \(\theta''\) : theta2, \(\theta'\) : theta1 を測地線の方程式に代入する:
\[
\theta'' - 2 \cot(\theta) (\theta')^2 - \cos(\theta)\sin(\theta) = 0
\]
theta2 - 2 * cot(theta) * (theta1)**2 - cos(theta) * sin(theta)
\[\displaystyle \left(2 \sin{\left(\theta{\left(t \right)} \right)} \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \omega{\left(t \right)}\right)^{2} - \frac{d^{2}}{d t^{2}} \omega{\left(t \right)}\right) \sin^{2}{\left(\theta{\left(t \right)} \right)} - 2 \sin^{4}{\left(\theta{\left(t \right)} \right)} \cot{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \omega{\left(t \right)}\right)^{2} - \sin{\left(\theta{\left(t \right)} \right)} \cos{\left(\theta{\left(t \right)} \right)}\]
式の簡略化に先立って、三角関数の倍角公式の適用を避けるため \(\sin^2(\theta)\) で割っておく:
sympy.expand(_ / sin(theta)**2)
\[\displaystyle - 2 \sin^{2}{\left(\theta{\left(t \right)} \right)} \cot{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \omega{\left(t \right)}\right)^{2} + 2 \sin{\left(\theta{\left(t \right)} \right)} \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \omega{\left(t \right)}\right)^{2} - \frac{d^{2}}{d t^{2}} \omega{\left(t \right)} - \frac{\cos{\left(\theta{\left(t \right)} \right)}}{\sin{\left(\theta{\left(t \right)} \right)}}\]
sympy.simplify(_)
\[\displaystyle - \frac{d^{2}}{d t^{2}} \omega{\left(t \right)} - \frac{1}{\tan{\left(\theta{\left(t \right)} \right)}}\]
\(\omega(t) = \cot(\theta(t))\) と置いていたので、測地線の方程式は次の微分方程式と等価になる:
\[
\omega''(t) + \omega(t) = 0
\]
微分方程式を解く:
t = Symbol('t')
omega = Function('omega')(t)
omega
\[\displaystyle \omega{\left(t \right)}\]
omega.diff().diff()
\[\displaystyle \frac{d^{2}}{d t^{2}} \omega{\left(t \right)}\]
from sympy.solvers import solve, dsolve
dsolve(omega.diff().diff() + omega, omega)
\[\displaystyle \omega{\left(t \right)} = C_{1} \sin{\left(t \right)} + C_{2} \cos{\left(t \right)}\]
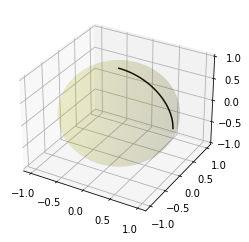
球面上の大円を表す方程式となる。
from scipy.spatial import geometric_slerp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import proj3d
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x = np.outer(np.cos(u), np.sin(v))
y = np.outer(np.sin(u), np.sin(v))
z = np.outer(np.ones(np.size(u)), np.cos(v))
ax.plot_surface(x, y, z, color='y', alpha=0.1)
start = np.array([1, 0, 0])
end = np.array([0, 0, 1])
t_vals = np.linspace(0, 1, 200)
result = geometric_slerp(start,
end,
t_vals)
ax.plot(result[...,0],
result[...,1],
result[...,2],
c='k')
#ax.set_aspect('equal')
plt.show()
